|
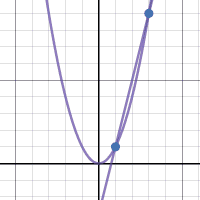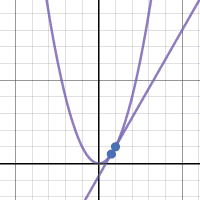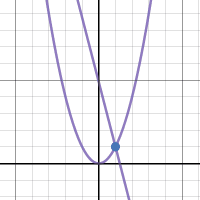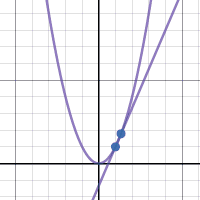
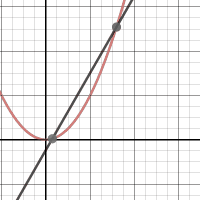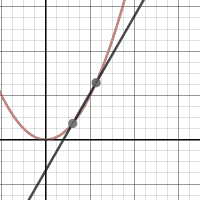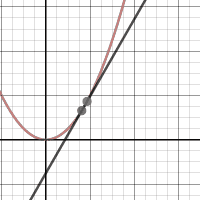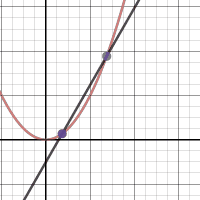
This week we had an activity where we created three GIFs, the three that I created are these: This week we had an activity where we created three GIFs, the three that I created are these: The first activity helped with the generalization represented in the first GIF by showing that the slope of a secant line will narrow down until you get to the point where the tangent line is. You can generalize the tangent’s slope by finding the slope of the secant lines that slowly get closer to the tangent line. The one thing that my whole table struggled with was not knowing exactly what tangent and secant lines were. We figured out how to do the generalization problem once we knew what they were. When making the first graph the one thing I struggled with doing was keeping the line at one point instead of having it move up and down the graph. I figured it out after talking it over with people. One change that had to be made from the first to second graph was to make the one stationary point a point that also moves. Instead of having the points for the slope be (a, f(a)) and (2,2) they became (a, f(a)) and (b, f(b)) for the slope equation m. I also had to write a separate equation for the line. The analysis of secant lines helps to determine the tangent line of a function by allowing for us to slide the line along the function until it is at the point of tangency and then the slope can be calculated and the equation for the line can be written.
0 Comments
Leave a Reply. |
Details
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
March 2017
Categories |
 RSS Feed
RSS Feed
