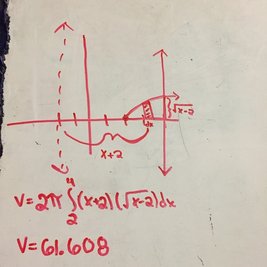
 We started off this week with the decision to take the disk and washer method quiz on Monday or Tuesday, obviously we chose Tuesday because a. We didn’t know there was supposed to be a test and b. I would have no clue what I was doing on that test if we took it Monday. I’m grateful that we took the test on Tuesday, but I really didn’t study as much as I could have. Starting the shell method also may have distracted me from the disk and washer methods, even though it wasn’t on the test my brain was trying to process new information that can be used to solve similar problems while at the same time trying to remember things that I had just learned. With that being said I think I did okay on the quiz. I understood the shell method pretty well when the rotations were happening about the x or y axis but when they were being rotated about a line that kinda threw me for a loop. On Thursday we did a few problems on the whiteboards that were being rotated about a line and that was really helpful and it allowed me to understand how to solve problems like that easier. It was also a helpful review in a way for the quiz that we took on Friday.
0 Comments
 This week we worked on 7.2 and started 7.3 and I realized that I really hate whiteboard starts where we have to work with people we don’t sit next to. The group that I have been put in for the past few whiteboard starts really doesn’t talk through how to figure out a problem, there are is one student who just takes control and does the problem without explaining what he is doing or his thought process. Maybe if they would explain what he was thinking I would grasp the new material being taught. I understand that this is an AP class so students should be able to understand things without them being explicitly said, but when things are just assumed that everyone understands and then moves on I don’t really follow and then I don’t grasp a concept until we have moved on. This week after the whiteboard start things we explained and not assumed which made the start to the chapter a lot smoother. There are still things that I’m working through because it takes me a while to process, but I have a much better grasp to the beginning of chapter 7 so hopefully I will have a better start to next trimester.  This week we wrapped up on chapter six and started chapter seven. I understood what I was doing during chapter six but there were also parts that I found difficult to grasp because I would get them mixed up in my mind. When defining the definite integral using u substitution I would forget to take the antiderivative in order to solve the integral. Once we began chapter seven thing began to seem clearer, and the things that we learned in chapter five as well. Everything keeps building on each other and at the time that I am learning it I struggle with it but once we start a new chapter and we build on it I start to understand. I think that I just need time to process what I’m learning and lately I have felt like somethings are just assumed to be known. Being able to talk through homework problems at my table is helpful to my understanding of the material because people are able to understand how to do math. Also seeing that others don’t completely understand everything is helpful just because sometimes I feel like I’m the only person that doesn’t know what is going on, so it is reassuring.  In learning the fundamental theorem of calculus I relied on both deductive and inductive reasoning. I did find it easier to use inductive reasoning more than deductive reasoning, just because it was easier to grasp what is being talked about. I usually learn better by seeing and then doing rather than being thrown a bone and left to fend for myself when being introduced to a new idea. I am able to learn on my own, but I do struggle when things are assumed to be understood and I don’t completely grasp the idea. As a dancer I am able to see what I am supposed to be doing and then I can recreate it myself. I have found over the years in math that once I have seen a certain type of problem I can do them and build upon them, I just need to see a basic example to get myself going. The fundamental theorem of calculus is so fundamental because it shows that every continuous function has an antiderivative, that the process of integration and differentiation are inverses of one another, and that definite integrals can be evaluated directly from the antiderivative of a function. Because this is known then you are able to find the integral of an equation much easier In my mind the fundamental theorem of calculus is still a little fuzzy. At times I completely understand it, but at other times I am completely lost. I know that it really is allowing for the area under a curve to be found, but it still is slightly difficult to grasp. This week was the first week back from break and I think that it could basically summarized in the four words, I'm going to die. After not doing much math, besides trying to figure out if I had lead my family on the 27 mile snowshoe trail or the 4 mile snowshoe trail at Tahquamenon Falls, it took a little while to understand what the heck I was supposed to be doing for the chapter four test.
I have learned after this week that it took us almost 6 weeks to get through a chapter and that the chapter reviews are generally much harder than the actual tests. The first 10-15 problems in the assignment were over the oldest material in the chapter and while the chapter does build on itself for the first 4ish sections the last few sections had nothing to do with those problems. The last few sections were what was slightly fresh in my brain, so the last half of the assignment wasn't very difficult. I felt a lot better on the second day back to class but I did still have a few moments where I thought I was going to die because it couldn't handle the types of mathematics it was being asked to do. However by Thursday I understood the majority of topics that were going to be on the test. After that I was okay, but I still slightly felt like I was going to die because I realized that we have no planned days off from school until spring break..  This week we went from optimization to related rates, and in the introduction to it Mr. Cresswell said usually students understand one more than the other. In my personal case I found this to not really be true, there were parts that I could do right like getting the picture drawn, but then figuring out what needed to be used as the mathematical model stumped me. Out of the six steps I can do 4 consistently, I can create a diagram, and label the known variables, I can plug in the variables, and I can solve for the last known variable. The last three parts are fine and dandy if I can use the right formula for the mathematical model. After writing the mathematical model finding the derivative is the next hardest part because I may or may not have blocked out how to do implicit differentiation. After looking back at my notes and practice with it through out this week I have gotten better at using implicit differentiation to take the derivative. After doing a lot of different problems I do feel that I have got a better handle on related rates problems. There may be a few conceptual gray areas with a couple of problems, but I do feel that I have a better grasp of things than I did last week, so maybe it does ring true that students are usually better at either optimization or related rates. This week was very interesting. I was really starting to feel a little overwhelmed with school and really wishing that thanksgiving break was longer or that winter break was sooner. I also noticed that missing the Friday before exams didn't really help for the start of this chapter. I was a little flustered when we got back to school just because I really didn't grasp the topic before break, so jumping right back into it and not understanding things made it a little difficult. However once we got to 4.3 I was able to grasp things a lot easier.
4.1 and 4.2 was just getting introduced to everything and then 4.3 brought everything together. It was also very helpful to do the curve analysis gallery walk, while doing it I found it a little difficult to visualize something in my mind without seeing it actually on paper/in picture. After doing the gallery walk the curve sketching activity was a breeze because I found it easier to visualize the first and second derivatives without actually drawing them out on paper. So I wasn’t really at school this week, I was there on Monday and Tuesday but I was gone the rest of the week. On Monday I was really grateful that we were able to have more practice with the chain rule because I understood it, but I just wanted more practice with it. The worksheet we got wasn’t too hard at first, but the further I got into it it became more difficult which I had mixed feelings about it. I liked it but there were somethings that took a little while to figure out how to solve it, so I guess it’s going to make me better at math but I don’t like it (kinda like little kids with vegetables).
I got the first part of the notes for part one of 3.7 and I didn’t have much trouble with implicit derivatives, it just takes me a while to do the problems. Being gone for the rest of the week I got the notes and didn’t struggle with it too much. The only thing that I’m worried about looking ahead is that I’m going to take to long with these new sections on the chapter test and run out of time, but practicing is really the only thing that will help me get faster at the problems. This week was probably the first week where I was a little lost. I understood the chain rule and anti-differentiation using “u” substitution and felt I understood it well in time for the mini-quiz, but leading up to it I didn’t understand it very well. The composition activity that we did on Monday I felt was a good lead up to the chain rule, but once we actually got to doing the chain rule with the product and quotient rules I found it a little more difficult to grasp. I think that it was more difficult because there’s so much to keep organized. At one point during class Mr. Cresswell told us that if we were having difficulty understanding what we were doing to take a break, because there’s no point in trying to work with a fried brain. I ended up saving the problems that I had left for homework, and I had a moment at home where it all clicked. That moment that clicked I was working on a chain rule problem with a power rule within it and I figured out the pattern that was used when finding the derivative. This week was a little more difficult than previous weeks, but I did eventually figure out things. I’m actually kind of glad that it was a little difficult because we’ve been doing derivatives for a while now and they were starting to get monotonous. The difficulty changed up the speed, so while I’m dreading working with derivatives for much longer I’m glad for the change in difficulty. How I feel when I find out we are still doing derivatives
 This week we started to learned different rules that will allow us to find the derivative of functions. The 4 rules that we learned in 3.3 are a really quick way to find the derivative, and it makes it a lot faster to find the derivative. In learning the quicker way to find the derivative, we were able to use other rules like the quotient and product rules to find the derivatives. We also learned how to find the original equation when we are given the derivative, without having to guess. This is also known as the anti-derivative. The one thing that I need to remember is to add ‘c’ at the end of the function. This ‘c’ is added because the derivative of a constant is zero, so we don’t see it when finding the anti-derivative. We also learned the derivatives/anti derivatives of trig functions. These are pretty easy because they are set values for each function, so you aren’t as likely to get numbers mixed up. They also simplify nicely, which make them kind of fun to do. We aren’t done with the chapter yet, so I can’t imagine what else we could so with derivatives. I’m not going to complain though, because they aren’t very difficult and I’m doing well in the class. |
Details
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
March 2017
Categories |




 RSS Feed
RSS Feed
